实验三：全源最短路¶

在本实验中，你将通过实现 GPU 加速的全源最短路（Floyd-Warshall 算法）熟悉 CUDA 编程，以及一种常见的优化方法：分块（Blocking）。在保证正确性的前提下，我们鼓励探索利用 GPU 的各种硬件特性以优化程序性能。

实验任务¶

你需要实现一个在 GPU 上运行的 Floyd-Warshall 算法。相信你在之前的课程中对 Floyd-Warshall 算法已经有所理解。如果你对图或全源最短路仍不太了解，可以通过书籍、博客与其他课程等多种途径进行学习。作为提醒，以下是 Floyd-Warshall 算法的伪代码：

// 设图 G = (V, E) 为赋权有向图
// 输入图的大小 |V| = n
// 输入邻接矩阵 D[n][n]，D[x][y] 表示点 x 到点 y 的距离
for (int k = 0; k < n; k++)
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            D[i][j] = min(D[i][j], D[i][k] + D[k][j]);

为简化问题，本实验中对输入作如下约定：

输入图 $G = (V, E)$ 的规模 $|V| <= 10000$ ；
$E$ 中的所有边权为整数，且不大于 $100000$ ；
$G$ 为完全图，即邻接矩阵中不存在值为无穷大的项；
$G$ 中，每个点到自己的距离保证为 $0$ 。

你需要修改 apsp.cu 文件以实现自己的算法。具体而言，你需要实现该文件中的 void apsp(int n, int *graph) 函数，其具体定义可以在 apsp.h 中找到。请注意 graph 指针指向 GPU 内存地址。除调试外，一般你不需要在主存和 GPU 内存之间进行拷贝。请在 graph 指针指向的邻接矩阵中 原地更新结果，不需要将结果写入其他数组。

apsp.cu 中已经包含了 Floyd-Warshall 算法的最简单的 GPU 实现，可作为参考，但仍有十几倍的优化空间。请不要修改除 apsp.cu 外的任何文件。

请注意：朴素的 GPU 实现难以发挥 GPU 的硬件优势（往往劣于 CPU 上的朴素 OpenMP 实现），针对 GPU 进行程序优化往往是必须的。因此，你必须对 GPU 实现进行优化（直接提交未经修改的 apsp.cu 将不会获得加速比得分）。下一节，我们提供了参考的优化方法。

参考优化方法¶

以下介绍一种基于分块思想的 Floyd-Warshall 算法优化方法，这种方法可以提升数据的局部性，以充分利用 GPU 的共享内存和寄存器资源。这种方法是本实验的推荐实现方法。如果你有更好的思路，也鼓励尝试其他优化策略。

设图 $G=(V,E)$ 的规模 $n = |V|$ ，邻接矩阵为矩阵 $D \in \mathbf{R}^{n \times n}$ ，首先将 $D$ 分为大小为 $b \times b$ 的块（即子矩阵）。如下图， $D$ 被分为了 $16$ 块。

图1：分块

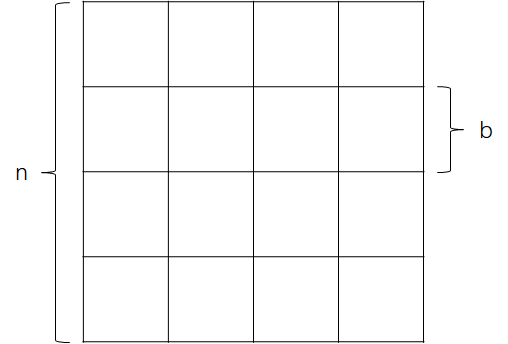
算法分为 $\lceil\frac{n}{b}\rceil$ 步，每步分为三阶段。第 $p$ 步（ $0 \le p < \lceil\frac{n}{b}\rceil$ ）对应于原算法中 $pb \le k < (p+1)b$ 的迭代。算法如下：

阶段一¶

选出对角线上的第 $p$ 个块，记为“中心块”。在中心块内部执行 Floyd-Warshall 算法。以 $p=1$ 为例，如下图：

中心块

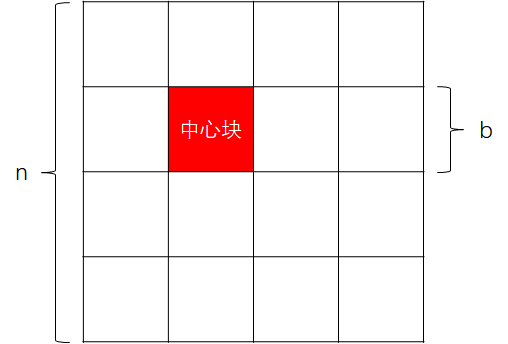
伪代码如下：

for (int k = p * b; k < (p + 1) * b; k++)
    for (int i = p * b; i < (p + 1) * b; i++)
        for (int j = p * b; j < (p + 1) * b; j++)
            D[i][j] = min(D[i][j], D[i][k] + D[k][j]);

阶段二¶

选出中心块上下左右方向的 $2(\lceil\frac{n}{b}\rceil - 1)$ 个块，记作“十字块”。用中心块的结果和十字块中原本的其他结果更新十字块。以 $p=1$ 为例，如下图：

十字块

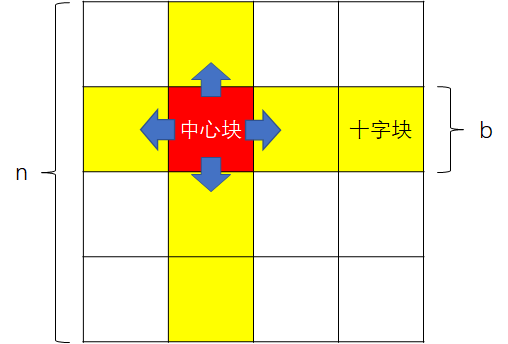
伪代码如下：

for (int k = p * b; k < (p + 1) * b; k++) {
    for (int i = p * b; i < (p + 1) * b; i++) {
        for (int j = 0; j < p * b; j++)
            D[i][j] = min(D[i][j], D[i][k] + D[k][j]);
        for (int j = (p + 1) * b; j < n; j++)
            D[i][j] = min(D[i][j], D[i][k] + D[k][j]);
    }
    for (int j = p * b; j < (p + 1) * b; j++) {
        for (int i = 0; i < p * b; i++)
            D[i][j] = min(D[i][j], D[i][k] + D[k][j]);
        for (int i = (p + 1) * b; i < n; i++)
            D[i][j] = min(D[i][j], D[i][k] + D[k][j]);
    }
}

阶段三¶

用“十字块”的结果更新剩余的块。以 $p=1$ 为例，如下图：

十字块

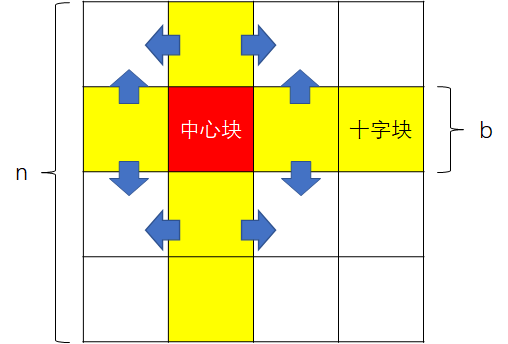
伪代码如下：

for (int k = p * b; k < (p + 1) * b; k++)
    for (int i, j ∈ [0, p * b) ∪ [(p + 1) * b, n))
        D[i][j] = min(D[i][j], D[i][k] + D[k][j]);

对于每个 $p$ ，依次执行上述三个阶段，即等价于原本的 Floyd-Warshall 算法。

利用这种分块的方式，你可以将部分数据放入大小有限的共享内存或寄存器中，以提升程序执行效率。

编程提示和优化技巧¶

使用分块算法时，矩阵底部和右侧的块可能是不完整的，在程序中可能需要边界判断；
使用指针时，请注意数据在 GPU 上还是主存上：本实验的输入输出均在 GPU 上，调试时你可能需要将其手动拷贝到主存上；
记得在适当位置添加 __syncthreads()（潜在优化点：最短路算法的某一步中，就算访问旧的 shared memory 值，也可证明答案是正确的，此时可以不做同步；如实现此项优化，鼓励在报告中提供证明）；
注意检查 kernel 和 CUDA API（例如 cudaMemcpy）调用中的错误（kernel 参数不合法、访存越界等错误时常体现为答案错误而非运行错误，此时需要注意排查）：
- 注意检查错误返回值（可使用 cuda_utils.h 中的 CHK_CUDA_ERR 宏）；
- 可使用 compute-sanitizer（旧称 cuda-memcheck）调试工具自动检查错误；
不需要 global memory 上的同步时，尽量将循环置于 kernel 内，以减少不必要的 kernel 启动次数；
调整 threadIdx.x 和 threadIdx.y 的顺序，或者调整数组的行优先/列优先方向，更好地适应全局内存的缓存行（cache line），以及避免（对性能的影响极其严重的）共享内存的 bank conflict 现象。
使用常量的线程块大小和共享内存大小，有助于编译器进行自动优化；
依据硬件资源进行调优：
- 调整分块大小和线程分配方案，尽可能用满 GPU 资源，包括线程数、共享内存大小、寄存器数量等，以提升性能；
- 可在P100 GPU 官方文档或NVIDIA提供的简易计算器查阅实验所用的 GPU 资源数量详情；
- 可以使用 nvprof 工具分析性能瓶颈：直接运行可获取各 kernel 的运行时间，详细性能指标可参阅 nvprof 支持的 event 和 metrics 列表，并在运行 nvprof 时指定该 event 或 metrics（访存数、缓存利用率等信息在 metrics 里，bacnk conflict 信息在 event 里）；
- 编译时可以使用 nvcc --ptxas-options=-v 命令打印 GPU 资源使用情况；由于在 CUDA 编程时没有办法规定一个变量一定要使用寄存器，而局部变量（含局部数组）既可能被编译为寄存器，也可能被编译为 local memory（即栈上内存）；这条命令有助于确认你的程序使用的到底是寄存器还是 local memory；如果你想使用寄存器却发现编译器使用了 local memory，请尝试 1）减少局部变量数目 2）减少访问局部变量时的相对访存；
- 注：课程集群提供的 P100 GPU 最大支持每个 SM 64KB shared memory，但每个 thread block 最多只支持 48KB，请勿混淆（文档）。

实验步骤¶

首先将实验文件 拷贝到自己的目录，并进入 PA3 目录：

cp -R /home/course/hpc/assignments/2023/PA3 ~/
cd ~/PA3/

修改 apsp.cu 文件以实现自己的算法。

编译运行流程¶

加载 CUDA 环境：spack load cuda；
编译：make；
运行 srun -p gpu -N 1 ./benchmark <图规模> 以运行你的程序。其中 <图规模> 为一个整数，表示图中的点数。程序会打印结果是否正确及运行时间两项数据。

分数细则¶

正确性¶

正确性得分共占 $60\%$ ，包含两部分：基础分（占 $10 \%$ ）和加速比得分（占 $50 \%$ ）。

对于基础分，如果 benchmark 程序输出了 Validation Passed，就可以获得该测试用例的基础分。有多组测试用例。你将获得通过的测试用例的分数，每个测试用例分数相同。

对于加速比得分，助教会使用图规模 $n = 10000$ （最大规模）运行你的程序，如果相对于助教提供的朴素实现（apsp_ref）的加速比 超过 2 ，则加速比合格，否则加速比不合格。对于每个测试用例，只有当你 获得了正确性基础分且加速比合格，方可获得该测试用例的加速比得分。注意，助教仅使用 $n = 10000$ 时的加速比来决定你的加速比是否合格，而不会对所有测试用例分别测试加速比。

参考依据

根据往年的评测结果，只要正确实现了上述的分块算法，将每个矩阵分块置于共享内存中，每个矩阵分块由一个线程块计算，即可达到 10 左右的加速比，远超加速比得分要求。

性能¶

性能得分共占 $30\%$ ，共有若干组 $n$ 不同的测试用例。

对于每组测试用例，只有当你获得了正确性基础分和加速比得分后，才能得到性能分。每组测试用例的性能分数相同。
性能测试只针对 void apsp(int n, int *graph) 函数。
根据你的性能在全体同学中的排名给出每组测试用例的分数：每组测试用例各自排名，性能排名前 $10 \%$ 的同学得到 $100 \%$ 的分数，排名 $10 \%$ - $20 \%$ 的同学得到 $90 \%$ 的分数，依此类推。对于任何测试用例，获得正确性分数的同学将至少获得 $10 \%$ 的性能分数。

得分建议

为了获得更高性能，最有效果的优化是实现两级分块。即每个大块置于共享内存中，各由一个线程块计算；每个小块至于寄存器中，各由一个线程计算。若实现了这种两级分块算法，并确保各线程每次可以访问连续若干个元素（以利用向量访存），就可以获得大幅性能提升。根据往年的评测结果，在 P100 （评测结点的 GPU）上， $n = 10000$ （最大规模）时，性能最高的提交的加速比可达 35 左右，其主要优化来源于两级分块。

实验报告¶

实验报告共占 $10\%$ ，助教根据实验报告给出分数，需要写的内容在“实验提交”一节中给出。

注意事项¶

禁止任何欺骗评测程序的手段，包括但不限于直接输出 Validation Passed、干扰校验程序运行、提前保存结果以在测试时直接输出等。一经发现，将取消本次实验得分。
你修改的文件应该仅限于 apsp.cu。即使修改了其他文件（如用于调试等目的），也要确保在 不进行这些修改 的情况下，程序能够正确编译运行。助教将替换所有其他文件为下发的版本后进行评测，以确保评分的正确性和公平性。
集群的登陆结点与计算结点配备了不同的 GPU，最终得分以计算结点为准（NVIDIA Tesla P100），程序在登陆结点的性能或正确性不作为评分依据。

实验提交¶

实验代码：
- 在截止日期之前将完成后的整个实验框架置于自己 home 目录下的 PA3 目录，如 /home/course/hpc/users/2020000000/PA3。
实验报告：
- 将 PDF 文件 提交至网络学堂。
- 包含以下内容：
  1. 介绍你的实现方法，包括有哪些 GPU kernel、每个 kernel 中线程和线程块如何分配、如何利用各级存储等（不要直接粘贴代码）；
  2. 在 $n = 1000, 2500, 5000, 7500, 10000$ 时的运行时间，及相对于助教提供的朴素实现的加速比。

最后更新: 2023年4月14日

作者: Harry Chen (6.7%), Shizhi Tang (89.39%), Harry Chen (1.12%), Shizhi Tang (2.23%), Jiajie Chen (0.56%)